If f;R to R is an odd function such that f(1+x)=1+f(x)and x^2f(1/x)=f(x) where x is not equal to zero find f(x)

Question

mycroft holmes · Answer

With the further assumption that f(x) is continuous, we can prove that f(x) = x is the only function satisfying the given conditions. (otherwise it becomes difficult to deal with transcendental reals). Proof: since the function is odd, we have f(0) = 0 and further f(-x) = -f(x), so it suffices to prove for x>0. 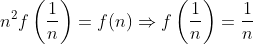By induction, we easily obtain from the 1 st condition that f(n) = n for any natural number n Now Now if x = 2/n with n>2, we have if n = 2k, x = 1/k and hence f(x) =f(1/k) = 1/k = x from the above result. Otherwise n = 2k+1, and f(n/2) = f(k+1/2) = k+f(1/2) = k+1/2 = (2k+1)/2 = n/2. Hence f(2/n) = (2/n) 2 (n/2) = 2/n. Now, let us look at x = 3/n, with n>3. If n=3k, then f(x)=x is evident. Else n = 3k+1 and using f(n/3) = f(k+1/3) we get f(x) = x Else n = 3k+2 and f(n/3) = f(k+2/3) and using the result we derived for f(2/n) we again have f(x) = x. So by strong induction, we can prove that f(m/n) = m/n i.e. f(x) = x for any . 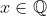Now, we take any irrational number x, and consider a sequence of rational numbers {q} that converges to x (just consider the decimal expansion of x for example). 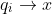By continuity (Heine Borel Theorem) since the we must have . 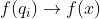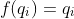But we have already proved that and hence limits are unique, we must have f(x) = x. Thus we have proved that f(x) = x for all x.

Thank you for registering.

Register Now and Win Upto 25% Scholorship for a Full Academic Year !

Enter Your Details

Registration done!

If f;R to R is an odd function such that f(1+x)=1+f(x)and x^2f(1/x)=f(x) where x is not equal to zero find f(x)

If f;R to R is an odd function such that f(1+x)=1+f(x)and x^2f(1/x)=f(x) where x is not equal to zero find f(x)

1 Answers

Think You Can Provide A Better Answer ?

Provide a better Answer & Earn Cool Goodies See our forum point policy

Other Related Questions on Algebra

ASK QUESTION

Answer and earn gift vouchers

View courses by askIITians

Design classes One-on-One in your own way with Top IITians/Medical Professionals

Complete Self Study Package designed by Industry Leading Experts

Live 1-1 coding classes to unleash the Creator in your Child

a Complete All-in-One Study package Fully Loaded inside a Tablet!

Register Now & Win Upto 25% Scholorship