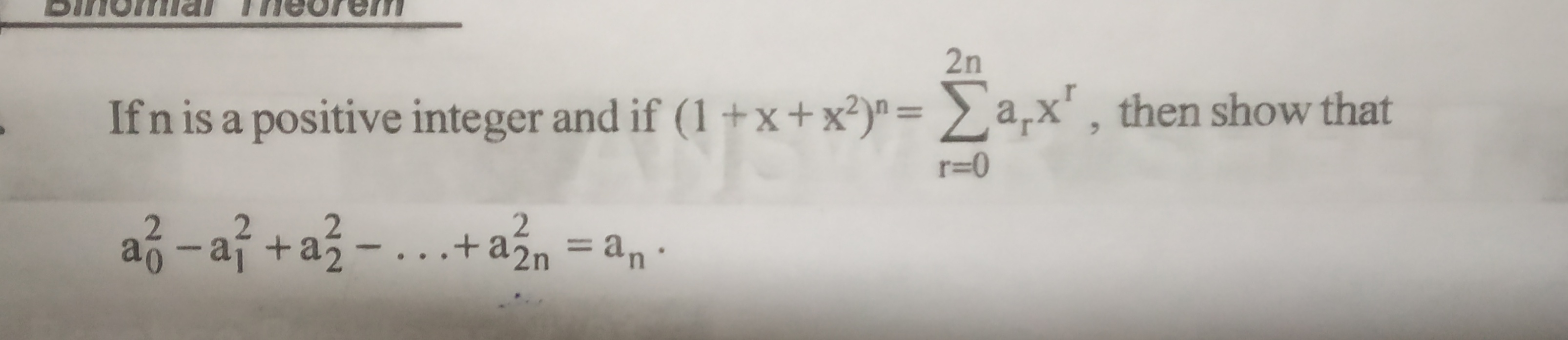if (1+x+x2)n = a0 +a1x +a2x2 + a3x3+ .......+ a2nx2n,show thata0^2-a1^2+a2^2-a3^2+...+a2n^2 = an
if (1+x+x2)n = a0 +a1x +a2x2 + a3x3+ .......+ a2nx2n,show thata0^2-a1^2+a2^2-a3^2+...+a2n^2 = an
Vaibhav , 6 Years ago
Grade 12th pass
Algebra> if (1+x+x2)n = a0 +a1x +a2x2 + a3x3+ .......
1 Answers
Aditya Gupta
Last Activity: 6 Years ago
(1+x+x2)n = a0 +a1x +a2x2 + a3x3+ .......+ a2nx2n... (1)
replace x by – 1/x
(1 – 1/x+1/x2)^n = a0 – a1/x +a2/x2 – a3/x3+ .......+ a2n/x2n
or (1 – x+x2)n = a0x^2n – a1x^(2n – 1) +a2x(2n – 2) – .......+ a2n... (2)
multiply 1 and 2
((1+x+x2)(1 – x+x2))^n= (a0 +a1x +a2x2 + a3x3+ .......+ a2nx2n)(a0x^2n – a1x^(2n – 1) +a2x(2n – 2) – .......+ a2n)
or (1+x^2+x^4)^n= (a0 +a1x +a2x2 + a3x3+ .......+ a2nx2n)(a0x^2n – a1x^(2n – 1) +a2x(2n – 2) – .......+ a2n)... (3)
now in 1, if we replace x by x^2, then we get
(1+x^2+x^4)^n= a0 +a1x^2 +a2x^4 + a3x^6+ .......+ a2nx^4n
put this value in 3,
a0 +a1x^2 +a2x^4 + a3x^6+ .......+ a2nx^4n= (a0 +a1x +a2x2 + a3x3+ .......+ a2nx2n)(a0x^2n – a1x^(2n – 1) +a2x(2n – 2) – .......+ a2n)
now consider the coefficient of x^2n on LHS. it is clearly an.
now consider the coefficient of x^2n on RHS. it is a0*a0+a1*( – a1)+a2*a2 – …..+a2n*a2n or a0^2-a1^2+a2^2-a3^2+...+a2n^2. since LHS=RHS, the coeffs on both sides should also equal each other.
hence a0^2-a1^2+a2^2-a3^2+...+a2n^2 = an
LIVE ONLINE CLASSES
Prepraring for the competition made easy just by live online class.
Full Live Access
Study Material
Live Doubts Solving
Daily Class Assignments
Other Related Questions on algebra
Can we divide two vectors? If this is possible then how?
Can we divide two vectors? If this is possible then how?
algebra
1 Answer Available
Last Activity: 1 Year ago
How do you write “the product of 18 and q” as an algebraic expression?
How do you write “the product of 18 and q” as an algebraic expression?
algebra
1 Answer Available
Last Activity: 1 Year ago
दहावीच्या आय सी एस इ विद्यार्थ्यांनी पुढे काय करायला पाहिजे
दहावीच्या आय सी एस इ विद्यार्थ्यांनी पुढे काय करायला पाहिजे
algebra
1 Answer Available
Last Activity: 2 Years ago