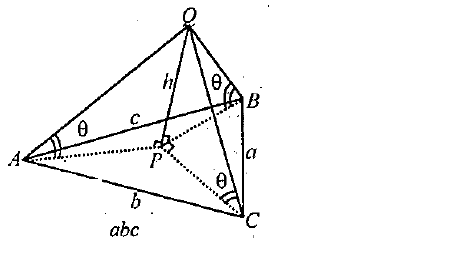
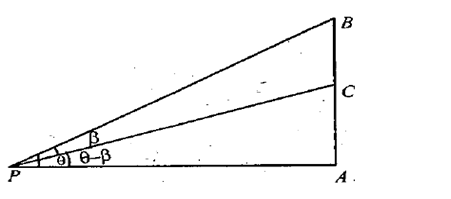
(i) PQ is a vertical tower. P is the foot and Q is the top of the tower. A, B, C are three points in the horizontal plane through P. The angles of elevation of Q from A, B, C are equal, and each is equal to θ. The sides of the triangle ABC are a, b, c and the area of the triangle ABC is ∆. Show that the height of the tower isabc tan θ/A∆(ii) AB is a vertical pole. The end A is on the level ground. C is the middle point of AB. P is a point on the level ground. The portion CB subtends an angle β at P. If AP = n AB, then show that tan β = n/2n2 + 1
(i) PQ is a vertical tower. P is the foot and Q is the top of the tower. A, B, C are three points in the horizontal plane through P. The angles of elevation of Q from A, B, C are equal, and each is equal to θ. The sides of the triangle ABC are a, b, c and the area of the triangle ABC is ∆. Show that the height of the tower is
abc tan θ/A∆
(ii) AB is a vertical pole. The end A is on the level ground. C is the middle point of AB. P is a point on the level ground. The portion CB subtends an angle β at P. If AP = n AB, then show that tan β = n/2n2 + 1