find all pairs of positive integers a,b such that a^b-b^a=3

Since RHS is odd, we must have either a is even and b is odd or vice versa.

 

Case I: a is even, b is odd

 

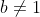
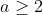
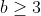
Also if , we must haveclearly, b>a. Hence  and hence . (In fact looking modulo 3, a is an even number of the form 3k+1, and hence the least value of a is 4, but that is not required here)

 

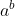
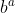
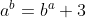
Now  will be of the form 8k, whereas  being the square of an odd number will be of the form 8k+1. So in the equation, LHS is of the form 8k while RHS is of the form 8k+4, which is a contradiction.

 

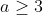
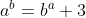
Case II: a is odd, b is even. Again, , So in the equation , LHS is of the form 8k+1 while RHS is of the form 8k+3 and so no solutions are possible.

 

That only leaves us with the possibility, b =1, in which case a = 4. Hence (4,1) is the only solution in natural numbers.