0

Guest

Courses New

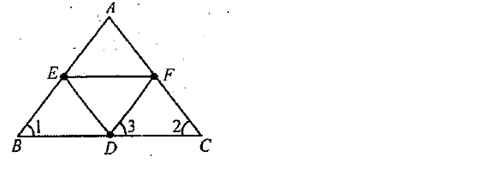
ABC is a triangle with AB = AC. D is any point on the side BC. E and F are point on the side AB and AC, respectively; such that DE is parallel to AC, and DE is parallel to AB Prove that DF + FA + AE + ED = AB + AC

ABC is a triangle with AB = AC. D is any point on the side BC. E and F are point on the side AB and AC, respectively; such that DE is parallel to AC, and DE is parallel to AB Prove that
DF + FA + AE + ED = AB + AC

Grade:11

1 Answers

Aditi Chauhan
askIITians Faculty 396 Points
9 years ago
Hello Student,
Please find the answer to your question
Given that AB = AC
∴ ∠1 = ∠2 . . . . . . . . . . . . . . . . . . . . . . (1)
236-2013_12345.png
But AB || DF (given ) and BC is transversal
∴ ∠1 = ∠3 . . . . . . . . . . . . . . . . . . . . . . . . . (2)
From equation (1) and (2)
∠2 = ∠3
⇒ DF = CF . . . . . . . . . . . . . . . . . . . . . . . (3)
Similarly we can prove
DE = BE
Now, DF + FA + AE +ED = CF + FA + AE + BE
= AC + AB [using equation (3) and (4)]

Thanks
Aditi Chauhan
askIITians Faculty

Think You Can Provide A Better Answer ?

Other Related Questions on Algebra

View all Questions »

ASK QUESTION

Get your questions answered by the expert for free

Answer and earn gift vouchers

Win Gift vouchers upto Rs 500/-

View courses by askIITians

Design classes One-on-One in your own way with Top IITians/Medical Professionals

Click Here Know More

Complete Self Study Package designed by Industry Leading Experts

Click Here Know More

Live 1-1 coding classes to unleash the Creator in your Child

Click Here Know More

a Complete All-in-One Study package Fully Loaded inside a Tablet!

Click Here Know More