Hey there! We receieved your request
Stay Tuned as we are going to contact you within 1 Hour
One of our academic counsellors will contact you within 1 working day.
Click to Chat
1800-5470-145
+91 7353221155
Use Coupon: CART20 and get 20% off on all online Study Material
Complete Your Registration (Step 2 of 2 )
Sit and relax as our customer representative will contact you within 1 business day
OTP to be sent to Change
Dear Shivramkrishna Singh,
The logarithm of a number is the exponent by which a fixed number, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: 1000 = 103 = 10 × 10 × 10. More generally, if x = by, then y is the logarithm of x to base b, and is written logb(x), solog10(1000) = 3.
Logarithms were introduced by John Napier in the early 17th century as a means to simplify calculations. They were rapidly adopted by scientists, engineers, and others to perform computations using slide rules and logarithm tables. These devices rely on the fact—important in its own right—that the logarithm of a product is the sum of the logarithms of the factors:
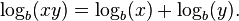
The present-day notion of logarithms comes from Leonard Euler, who connected them to the exponential function in the 18th century.
The logarithm to base b = 10 is called the common logarithm and has many applications in science and engineering. The natural logarithm has the constant e (≈ 2.718) as its base; its use is widespread in pure mathematics, especially calculus. The binary logarithm uses base b = 2 and is prominent in computer science.
Logarithmic scales reduce wide-ranging quantities to smaller scopes. For example, the decibel is a logarithmic unit quantifying sound pressure and voltage ratios. In chemistry, pH is a logarithmic measure for the acidity of an aqueous solution. Logarithms are commonplace in scientific formulas, and in measurements of the complexity of algorithms and of geometric objects called fractals. They describe musical intervals, appear in formulas counting prime numbers, inform some models in psychophysics, and can aid in forensic accounting.
In the same way as the logarithm reverses exponentiation, the complex logarithm is the inverse function of the exponential function applied tocomplex numbers. The discrete logarithm is another variant; it has applications in public-key cryptography.
Hope this helped you dear........
All the best.......
Please approve my answer by clicking 'Yes' given below, if you loved it......... Plz. Plz. Plz. don't forget to do it.....
Get your questions answered by the expert for free
You will get reply from our expert in sometime.
We will notify you when Our expert answers your question. To View your Question
Win Gift vouchers upto Rs 500/-
Register Yourself for a FREE Demo Class by Top IITians & Medical Experts Today !