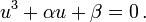Solving a quartic equation
Special cases
Consider the quartic

If
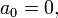
then
 ,
,
so zero is a root. To find the other roots, we can divide by  and solve the resultin cubic equation
and solve the resultin cubic equation

Evident roots: 1 and −1 and −k
If
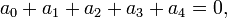
then
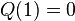 ,
,
so 1 is a root. Similarly, if
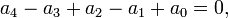
that is,

then -1 is a root.
When 1 is a root, we can divide
 by
by 
and get
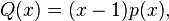
where  is a cubic polynomial, which may be solved to find
is a cubic polynomial, which may be solved to find 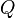 's other roots. Similarly, if -1 is a root,
's other roots. Similarly, if -1 is a root,

where  is some cubic polynomial.
is some cubic polynomial.
If

then −k is a root and we can factor out 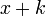 ,
,

And if

then both  and
and 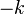 are roots Now we can factor out
are roots Now we can factor out  and get
and get

To get Q 's other roots, we simply solve the quadratic factor.
Biquadratic equations
If  then
then

We call such a polynomial a biquadratic, which is easy to solve.
Let 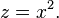 Then Q becomes a quadratic q in z,
Then Q becomes a quadratic q in z,
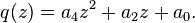
Let  and
and  be the roots of q. Then the roots of our quartic Q are
be the roots of q. Then the roots of our quartic Q are

Quasi-symmetric equations

Steps:
1) Divide by x 2.
2) Use variable change z = x + m/x.
The general case, along Ferrari's lines
To begin, the quartic must first be converted to a depressed quartic.
Converting to a depressed quartic
Let

be the general quartic equation which it is desired to solve. Divide both sides by A,

The first step should be to eliminate the x3 term. To do this, change variables from x to u, such that
 .
.
Then

Expanding the powers of the binomials produces

Collecting the same powers of u yields
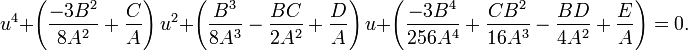
Now rename the coefficients of u. Let
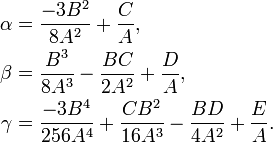
The resulting equation is
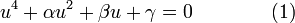
which is a depressed quartic equation.
If  then we have a biquadratic Equation, which (as explained above) is easily solved; using reverse substitution we can find our values for x.
then we have a biquadratic Equation, which (as explained above) is easily solved; using reverse substitution we can find our values for x.
If  then one of the roots is
then one of the roots is  and the other roots can be found by dividing by u, and solving the resulting equation,
and the other roots can be found by dividing by u, and solving the resulting equation,
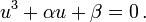
Using reverse substitution we can find our values for x.
Regards,
Rajat,
Askiitians Expert











 ,
, and solve the resultin cubic equation
and solve the resultin cubic equation
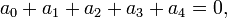
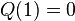 ,
, 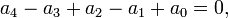

 by
by 
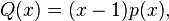
 is a cubic polynomial, which may be solved to find
is a cubic polynomial, which may be solved to find 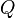 's other roots. Similarly, if -1 is a root,
's other roots. Similarly, if -1 is a root,

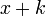 ,
,

 and
and 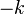 are roots Now we can factor out
are roots Now we can factor out  and get
and get
 then
then
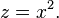 Then Q becomes a quadratic q in z,
Then Q becomes a quadratic q in z,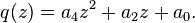
 and
and  be the roots of q. Then the roots of our quartic Q are
be the roots of q. Then the roots of our quartic Q are



 .
.

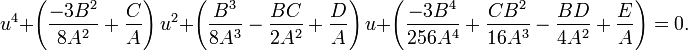
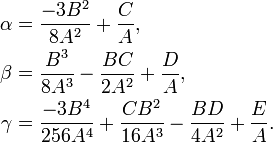
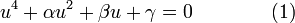
 then we have a biquadratic Equation, which (as explained above) is easily solved; using reverse substitution we can find our values for
then we have a biquadratic Equation, which (as explained above) is easily solved; using reverse substitution we can find our values for  then one of the roots is
then one of the roots is  and the other roots can be found by dividing by
and the other roots can be found by dividing by