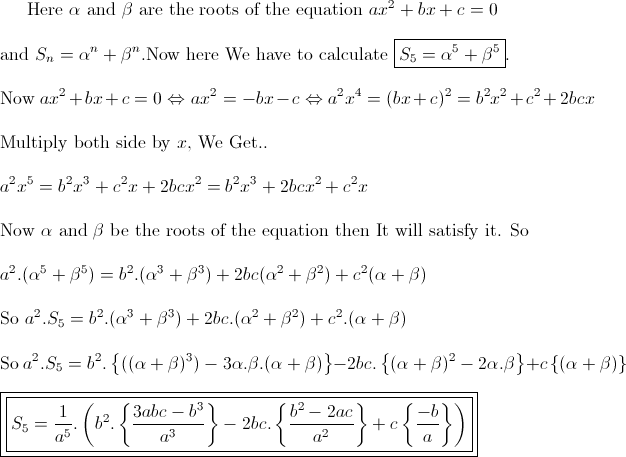If alpha and beta are the roots of the equation ax2 + bx + c = 0 and Sn = (alpha)n + (beta)n, show thataSn+1 + bSn + cSn-1 = 0 and hence find S5.

alfa = p    &   beta = q

aS_n+1 +bS_n + cS_n-1 = 0

taking LHS

= a(pⁿ⁺¹ + qⁿ⁺¹)+b(pⁿ+qⁿ)+c(p^n-1+ q^n-1)

=[apⁿ⁺¹+bpⁿ+cp^n-1] + [aqⁿ⁺¹+bqⁿ+cq^n-1]

=p^n-1[ap²+bp+c]  + q^n-1[aq²+bq+c]

now since p,q are the roots of eq ax²+bx+c=0 so  p,q  will satisfy this eq &

ap²+bp+c = 0 = aq²+bq+c

so the LHS becomes

LHS = 0+0 =0 =RHS

hence proved