AIPMT> There are 2 formulas for escape vel,in wh...

There are 2 formulas for escape vel,in what condition should we use the first formula and where should we use the second

liza , 5 Years ago

Grade 11

2 Answers

Saurabh Koranglekar

Last Activity: 5 Years ago

Dear student

https://www.askiitians.com/forums/Mechanics/10/28695/gravity.htm

please find the link

Approved

Rajdeep

Last Activity: 5 Years ago

HELLO THERE!

There are two formulas, that’s correct! But both are inter-related. Here I’m showing you how to derive the second formula from the first one.

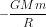
We know, that Gravitational Potention Energy (U) = $-\frac{GMm}{R}$

where, M = mass of Earth, m = mass of the satellite (or escaping object), and R = Radius of Earth.

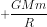
And, escape energy (E) = $+\frac{GMm}{R}$

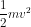
Let the escape velocity of the satellite be v, then it’s Kinetic energy = $\frac{1}{2}mv^{2}$

Now, this Kinetic energy = Escape energy when the satellite is escaping.

So,

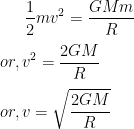
$\frac{1}{2}mv^{2} = \frac{GMm}{R} \\\\or, v^{2} = \frac{2GM}{R} \\\\or, v = \sqrt{\frac{2GM}{R}}$ ….....(i)

This is the first formula.

Now, from the relation between G (Universal Gravitational Constant) and g (acceleration due to gravity), we know that:

$g = \sqrt{\frac{GM}{R^{2}}}$

Let’s modify the first formula that we have obtained (Equation 1):

We have,

$v = \sqrt{\frac{2GM}{R}} \\\\= \sqrt{\frac{2GM}{R^{2}}\times R} \\\\= \sqrt{2gR}$

So, these are the two formulas, and you need to use them according to the data given in the question. If only the radius of earth (or radius of the planet from which the object is escaping is given, then you can use the second formula). If the mass of the earth or the planet from which the object is leaving is given, the first formula can be used. G has a constant value.

HOPE MY ANSWER IS SATISFACTORY...

Thanks!