0

Guest

Courses New

prove that angle bisectors of a triangle are concurrent

prove that angle bisectors of a triangle are concurrent

Grade:9

1 Answers

SHAIK AASIF AHAMED
askIITians Faculty 74 Points
9 years ago
Hello student,
Please find the answer to your question below
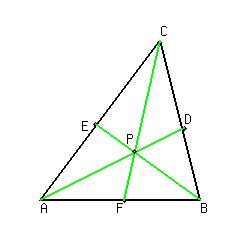
Figure 1shows the triangleABCwith the angle bisectorsAD,
BEandCFof its three anglesA,BandCrespectively. The
pointsD,EandFare the intersection points of the angle
bisectors and the opposite triangle sides.
Since the straight linesADandBEare the angle bisectors
to the anglesAandBrespectively, they can not be parallel,
otherwise the sidesABandBCwould be in one straight line
what is not the case. Therefore, the straight linesADand
BEintersect in some pointP.
From the lessonAn angle bisector properties(Theorem 1)
we know that the points of the angle bisectorADare
equidistant from the sidesABandACof the angleBAC.
Figure 1. To theTheorem
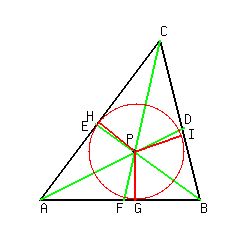
Figure 2. To the proof of theTheorem
In particular, the pointPis equidistant from the sidesABandACof the angleBAC. This means that the perpendicularsGPandHP(Figure 2) drawn from the pointPto
the sidesABandACare of equal length:GP=HP.

By the same reason, the points of the angle bisectorBEare equidistant from the sidesABandBCof the angleABC. In particular, the pointPis equidistant from
the sidesABandBCof the angleABC. This means that the perpendicularsGPandIP(Figure 2) drawn from the pointPto the sidesABandBCare of equal length:GP=IP.

Two equalities above imply that the perpendicularsHPandIPare of equal length too:HP=IP. In other words, the pointPis equidistant from the sidesACandBCof the
angleACB. In turn, it implies that the intersection pointPlies at the angle bisectorCFof the angleACBin accordance to theTheorem 2of the lesson
An angle bisector properties. In other words, the angle bisectorCFof the angleACBpasses through the pointP.

Thus, we have proved that all three angle bisectorsDG,EHandFIpass through the pointPand have this point as their common intersection point.
Since the pointPis equidistant from the triangle sidesAB,BCandAC, it is the center of the inscribed circle of the triangleABC(Figure 2).
So, all the statements of theTheoremare proved.
The proved property provides the way of constructing an inscribed circle for a given triangle.
To find the center of such a circle, it is enough to construct the angle bisectors of any two triangle angles and identify their intersection point. This intersection point
is the center of the inscribed circle of the triangle. To get the radius of the inscribed circle you should to construct the perpendicular from the found center of the
inscribed circle to any triangle side.240-1704_plot-formula.jpg240-1264_plot-formula (1).jpg

Think You Can Provide A Better Answer ?

Other Related Questions on 9 grade maths

View all Questions »

ASK QUESTION

Get your questions answered by the expert for free

Answer and earn gift vouchers

Win Gift vouchers upto Rs 500/-

View courses by askIITians

Design classes One-on-One in your own way with Top IITians/Medical Professionals

Click Here Know More

Complete Self Study Package designed by Industry Leading Experts

Click Here Know More

Live 1-1 coding classes to unleash the Creator in your Child

Click Here Know More

a Complete All-in-One Study package Fully Loaded inside a Tablet!

Click Here Know More