Ask a Doubt
Get your questions answered by the expert for free
Enter text here...
Other Related Questions on 10 grade maths

What are the advantages and disadvantages of mean, median and mode?
10 grade maths
1 Answer Available
Last Activity: 1 Year ago

Find the sum of the first 100 natural numbers.
10 grade maths
1 Answer Available
Last Activity: 2 Years ago

AOBC is a rectangle whose three vertices are A(0,-3), O(0,0) and B (4,0). The length of its diagonal is__
10 grade maths
1 Answer Available
Last Activity: 2 Years ago

For an AP, it is given that first term (a)= 5 and Common Difference (d) = 3 and nth term = 50. Find n and sum of first n terms of AP
10 grade maths
1 Answer Available
Last Activity: 2 Years ago

The value(s) of k for which the quadratic equation 2x^2 + kx + 2 = 0 has equal roots, is (a) 4 (b) pm 4 (c) -4 (d) 0
10 grade maths
1 Answer Available
Last Activity: 2 Years ago






 PAD=
PAD= So tan
So tan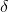 APD
APD )
)



