1800-150-456-789
FlagBACK
Flag 10 grade maths> Find the coorddinates of the point of int...
question mark

Find the coorddinates of the point of intersection of the straight lines 2x-3y=1 and 5y-x=3 and determine the angle between them

samaira , 5 Years ago
Grade 10
anser 3 Answers
Aditya Gupta

Last Activity: 5 Years ago

to find the point of intersection simply solve the two eqns together. 2x-3y=1 and 5y-x=3 gives x= 2 and y= 1.
so coordinates of the point of intersection= (2, 1)
now, the formula for angle between 2 lines is 
theta= arctan[|(m1 – m2)/(1+m1*m2)|], where m1 and m2 are the slopes of the lines.
here, m1= 2/3 for 2x-3y=1 and m2= 1/5 for 5y-x=3.
so, theta= arctan[|(m1 – m2)/(1+m1*m2)|]= arctan(7/17) which is approx 22.38 degrees.
kindly approve :)

Vikas TU

Last Activity: 5 Years ago

Dear student 
in equation 1 , a1 = 2 , b1 = -3 , 
in equation 2 a2 = 5 , b2 = -1 
a1/a2 is not equal to b1 / b2 
so, this is the condition of line to intersect , 
and angle between them = 22.38 degree.

Pawan Kumar Karela

Last Activity: 5 Years ago

Given equation    2x-3y=1   (1)
                            5y-x=3     (2)
we use the elimination method to get the intersection point.
therefore multiply equation (2) by 2 and then add it to equation (1) to eliminate variable y.
                          2x-3y=1     (3)
                         -2x+10y=6  (4)
adding (3) and (4) we get 
                            7y=7
                           y=1      (*)
              use value of y to get x
                     2x-3*1=1
                        2x=1+3
                         x=2
         therefore point of intersection is (2,1)
 
to find angle between these two lines we use formula
                                  tan\Theta =\left | \frac{m1-m2}{1+m1*m2} \right |
from equation (1)  2x-3y=1...... implies y=(2/3)x-1
                                                      therefore m1=2/3
similarly for equation (2)  y=1/5+3/5
                                       therefore m2=1/5
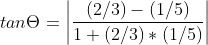
               hence tan\Theta =\left | \frac{(2/3)-(1/5)}{1+(2/3)*(1/5)} \right |
                           therefore on solving we get
                                      tan\Theta =\left | \frac{7}{17}\right |
                                       \Theta =tan^-1\left | \frac{7}{17}\right |

star
LIVE ONLINE CLASSES

Prepraring for the competition made easy just by live online class.

tv

Full Live Access

material

Study Material

removal

Live Doubts Solving

assignment

Daily Class Assignments


Other Related Questions on 10 grade maths

question mark
What are the advantages and disadvantages of mean, median and mode?
10 grade maths
1 Answer Available

Last Activity: 2 Years ago

question mark
Find the sum of the first 100 natural numbers.
10 grade maths
1 Answer Available

Last Activity: 3 Years ago

question mark
AOBC is a rectangle whose three vertices are A(0,-3), O(0,0) and B (4,0). The length of its diagonal is__
10 grade maths
1 Answer Available

Last Activity: 3 Years ago

question mark
For an AP, it is given that first term (a)= 5 and Common Difference (d) = 3 and nth term = 50. Find n and sum of first n terms of AP
10 grade maths
1 Answer Available

Last Activity: 3 Years ago

question mark
The value(s) of k for which the quadratic equation 2x^2 + kx + 2 = 0 has equal roots, is (a) 4 (b) pm 4 (c) -4 (d) 0
10 grade maths
1 Answer Available

Last Activity: 3 Years ago