A rectangular park 60 m long and 40 m wide has two concrete crossroads running in themiddle of the park and rest of the park has been used as a lawn. The area of the lawnis 2109 sq. m. what is the width of the road?A. 5 mB. 4 mC. 2 mD. 3 m

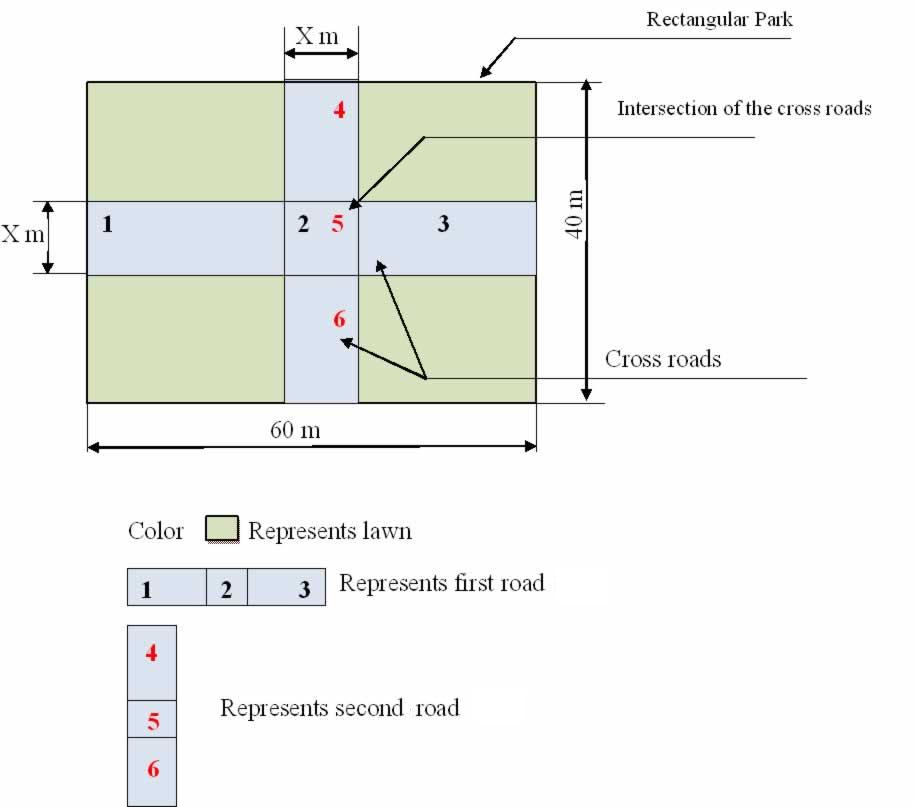
Please refer the diagram given above.

Area of the park = 60 × 40 = 2400 m²
Given that area of the lawn = 2109 m²
∴ Area of the cross roads = 2400 - 2109 = 291 m²

Assume that the width of the cross roads = x

Then total area of the cross roads
= Area of road 1 + area of road 2 - (Common Area of the cross roads)
= 60x + 40x - x²

(Let''s look in detail how we got the total area of the cross roads as 60x + 40x - x²
As shown in the diagram, area of the road 1 = 60x. This has the areas of the
parts 1,2 and 3 given in the diagram

Area of the road 2 = 40x. This has the parts 4, 5 and 6

You can see that there is an area which is intersecting (i.e. part 2 and part 5)
and the intersection area = x².

Since 60x + 40x covers the intersecting area (x²) two times ( part 2 and part 5)
,we need to subtract the intersecting area of (x²) once time to get the total area.
. Hence total area of the cross roads = 60x + 40x - x²)

Now, we have
Total areas of cross roads = 60x + 40x - x²
But area of the cross roads = 291 m²
Hence 60x + 40x - x² = 291
=> 100x - x² = 291
=> x² - 100x + 291 = 0
=> (x - 97)(x - 3) = 0
=> x = 3 (x can not be 97 as the park is only 60 m long and 40 m wide)