Relative Motion

Table of Content

Relative Velocity
Physical Significance of Relative Velocity
Relative Motion between Rain and Man
Relative Motion of a Swimmer in Flowing Water
Crossing of the River in Minimum Time
Velocity of Separation / Approach, Relative Angular Velocity
Related Resources

Relative Velocity

Relative Velocity Between Two Cars

In spite of our best efforts we could not find a fixed point with respect to which we should study absolute rest and absolute motion. So, the study of relative rest and relative motion assumes importance.

Consider two cars A and B running parallel to each other on same road with same velocities. No doubt the speedo meter of each indicates motion but the two drivers will always find themselves facing each other.

Relative velocity of a body A with respect to another body B, when both are in motion, is the velocity with which A appears to move to B.

The position, velocity and acceleration of a particle depend on the reference frame chosen.

A particle P is moving and is observed from two frames S and S'. The frame S is stationary and the frame S' is in motion.

Let at any time position vector of the particle P with respect to S is,

Position Vector of the Particle P with Respect to S

vector-OP

Position vector of the origin of S' with respect to S is,

sym1

From vector triangle OO'P, we get,

calculation

Physical Significance of Relative Velocity

Relative Velocity When Two Car Moving in Same Direction

Let two cars move unidirectional. Two persons A and B are sitting in the vehicles as shown in figure. Assume, V_A = 10 m/s & V_B = 4 m/s. The person A notices person B to be moving towards him with a speed of (10-4) m/s = 6 m/sec. That is the velocity of B with respect to (or relative to) A. That means $\vec{v}_{BA}$ is directed from B to A.

Similarly A seems to move towards B with a speed 6 m/sec. That means the velocity of A relative to B ( $\vec{v}_{AB}$ ) has the magnitude 6 m/sec & directed from A to B as shown in the figure.

Vectorical Representation of Relative Velocity When Two Car Moving

Therefore,

$\vec{v}_{AB}=-\vec{v}_{BA}$

In general, $\vec{v}_{BA} = \vec{v}_{B}-\vec{v}_{A}$

So,

$\left | \vec{v}_{BA} \right |=\left | \vec{v}_{AB} \right |$

v_AB = √ v_A² + v_B²- 2v_Av_Bcosθ

and θ = tan^-1{(v_Bsinθ)/(v_A – v_Bcosθ)}

Relative Motion between Rain and Man

Direction of Rain Fall as Seen by the Moving Man

We know that, v_r = v_rg = velocity of rain w.r.t. ground, v_m ≡ v_mg.

Velocity of man w.r.t. ground and

$\vec{v}_{rm}=\vec{v}_{rm}-\vec{v}_{m}$

velocity of rain w.r.t. man.

So, $\vec{v}_{r}=\vec{v}_{rm}+\vec{v}_{m}$

That means the vector addition of the velocity of rain with respect of man ( $\vec{v}_{rm}$ ) and the velocity of man (vehicle) ( $\vec{v}_{m}$ ) yield the actual velocity of rain $\vec{v}_{r}$ . The magnitude and direction of $\vec{v}_{r}$ can be given as,

v_r = √((v_rm)²+(v_m)²+ 2v_rm v_m cosθ)

? = tan^-1((v_rm sinθ)/(v_rm cosθ+ v_m )) with horizontal $\vec{v}_{m}$

Direction of Rain Fall as Seen by the Stationary Man (Actual Direction of Rain Fall)

Illustration (JEE Main):

Four particles A, B, C and D are in motion. The velocities of one with respect to other are given as $\vec{v}_{DC}$ is 20 m/s towards north, $\vec{v}_{BC}$ is 20 m/s towards east and $\vec{v}_{BA}$ is 20 m/s towards south. Then $\vec{v}_{DA}$ is

(a) 20 m/s towards north

(b) 20 m/s towards south

(d) 20 m/s towards west

Solution:

From the question, we know that,

$\vec{v}_{DC} = \vec{v}_{D} - \vec{v}_{C} = 20\hat{j}$ …... (1)

$\vec{v}_{BC} = \vec{v}_{B} - \vec{v}_{C} = 20\hat{i}$ …... (2)

$\vec{v}_{BA} = \vec{v}_{B} - \vec{v}_{A} = - 20\hat{j}$ …... (3)

Equation (1) – (2) + (3) gives:

$\vec{v}_{D} - \vec{v}_{A} = - 20\hat{j}$

or $\vec{v}_{DA} = - 20\hat{i}$

That is, $\vec{v}_{DA}$ is 20 m/s towards west.

Thus from the above observation we conclude that, option (d) is correct.

Illustration:

A stationary person observes that rain is falling vertically down at 30 km/hr. A cyclist is moving on the level road, at 10 km/hr. In which direction should the cyclist hold his umbrella to project himself from rain?

Solution:

Relative to stationary frame, velocity of rain is 30 km/hr downward. Take horizontal axis as x-axis and vertical axis as y-axis and i,j are the unit vectors along x and y axes respectively.

Vector Diagram of Cyclist and Rain Fall

$\vec{v}_{R}$ = 0-30j, $\vec{v}_{c}$ = 10î

$\vec{v}_{R,c} =\vec{v}_{R}-\vec{v}_{c}$

= -30j - 10i = -10i - 30j

If angle between horizontal and $\vec{v}_{R,c}$ is θ, then,

tan θ = -30/-10 = 3

=> θ = tan^-1 3 => θ=72°
Therefore, to protect himself from rain the cyclist should hold the umbrella at an angle of 72° from horizontal.

Illustration:

A man walking eastward at 5 m/s observes that wind is blowing from the north. On doubling his speed eastward, he observes that wind is blowing from north-east. Find the velocity of the wind.

Solution:

Let velocity of the wind is,

v_w=(v₁i+v₂j)m/s

And velocity of the man is,

v_m=5i

So, v_wm = v_w- v_m=(v₁-5)i + v₂j

In first case,

v₁- 5 = 0 => v₁= 5 m/s.

In the second case, tan 45^o = v₂/(v₁- 10)

=> v₂= v₁ - 10 = -5 m/s.

=> v_w= (5i - 5j) m/s.

Illustration:

From a lift moving upward with a uniform acceleration 'a', a man throws a ball vertically upwards with a velocity v relative to the lift. The ball comes back to the man after a time t.

Show that a + g = 2 v/t

Solution:

Let us consider all the motion from lift frame. Then the acceleration, displacement and velocity everything will be considered from the lift frame itself. As the ball comes back to the man, therefore displacement from the lift frame is zero. Again, the velocity with respect to the lift frame is v.

g - (-a) = a + g (↓) downwards

Now, s = ut + 1/2at² => 0 = vt - 1/2 (a+g)t²

or a + g = 2(v/t) .

Relative Motion of a Swimmer in Flowing Water

Take $\vec{v}_{m}$ = velocity of man

$\vec{v}_{w}$ = velocity of flow of river,

Relative Motion of Swimmer

$\vec{v}_{mw}$ = velocity of swimmer w.r.t. river

$\vec{v}_{m}$ can be found by the velocity addition of $\vec{v}_{mw}$ and $\vec{v}_{w}$ .

vectors

Crossing of the River with Minimum Drift

Case 1: v_mw > w

A man intends to reach the opposite bank at the point directly opposite to the stationary point. He has to swim at angle θ with a given speed $\vec{v}_{mw}$ w.r.t. water, such that his actual velocity $\vec{v}_{m}$ will direct along AB, that is perpendicular to the bank (or velocity of water $\vec{v}_{w}$ ).

=> For minimum drift, $\vec{v}_{m}$ ⊥ $\vec{v}_{w}$ Relative Motion of Swimmer (Case-1)

You can realize the situation by a simple example. If you want to reach the directly opposite point or cross the river perpendicularly, a man, that is to say, Hari, must report you that, you are moving perpendicular to the shore. What does this report signify? Since Hari observes your actual velocity ( $\vec{v}_{m}$ ) to be perpendicular to the bank $\vec{v}_{m}$ is perpendicular to $\vec{v}_{w}$ .

Observing the vector-triangle v_w = v_mw sinθ & v_m = v_mw cosθ

=> θ = sin^-1(v_w/v_mw ) & v_m = √((v_mw )²- (v_w)²)

=> The time of crossing, t = d/v_m

=> t = d/√(v_mw )² - (v_w)²)

Case 2 : v_w > v_mw

Let the man swim at an angle θ’ with normal to the bank for minimum drift. Suppose the drift is equal to zero. For zero drift, the velocity of the man along the bank must be zero.

=> v_m= v_w- v_mw sin θ' = 0

This gives, sinθ' = v_w / v_mw, since v_w > v_mw, sinθ' > 1 which is impossible. Therefore, the drift cannot be zero.

Now, let the man swim at an angle θ with the normal to the bank to experience minimum drift. Suppose that the drifting of the man during time t when the reaches the opposite bank is,
Velocity of the Man

BC = x

x = (v_m)x (t) … (1)

where t = AB/((v_m )y cosθ) = d/(v_mw cosθ) … (2)

and (v_m)x = v_w – v_mw sin θ … (3)

Using (1), (2) & (3), we obtain

x = (v_w- v_mw sinθ d/(v_mw cosθ))

Relative Motion of Swimmer (For x to be Minimum)

= (v_w/v_mw sec θ-tanθ)d

x = (v_w/v_mw sec θ-tanθ)d … (4)

For x to be minimum,

dx/dθ = (v_w/v_mw secθ - tanθ - sec²θ)d = 0

v_w/v_mw tanθ = (sec θ) => sinθ = v_mw/v_w

θ = sin-1(v_mw/v_w)

Substituting the value of θ in (4), we obtain,

x = [√(v_w² – v_mw²)/v_mw] d

Refer this video for more about Relative Velocity

Crossing of the River in Minimum Time

Case 1: To reach the opposite bank for a given v_mw

Let the man swim at an angle θ with AB. We know that the component of the velocity of man along shore is not responsible for its crossing the river. Only the component of velocity of man (v_m) along AB is responsible for its crossing along AB.

The time of crossing = t = AB/(v_mw cosθ)

Time is minimum when cos θ is maximum.

Time of Crossing

The maximum value of cos θ is 1 for θ = 0.

That means the man should swim perpendicular to the shore.

=> v-vector mw ⊥ w

=> Then t_min = d/(v_mw cosθ)|(θ=0) = d/v_mw => t_min= d/v_mw

Case 2:

To reach directly opposite point on the other bank for a given v_mw & velocity v of walking along the shore.

To attain the direct opposite point B in the minimum time, let the man swim at an angle θ with the direction AB. The total time of journey t = the time taken from A to C and the time taken from C to B.

=> t = t_AC + t_CB

where t_AC = AB/v_mvcosθ & t_CB = BC/v where v = walking speed of the man from C to B.

=> t = AB/v_mvcosθ + BC/v

Again BC = (v_m)_xt

=> BC = (v_w - v_mwsinθ) (AB/v_mwcosθ)

Using (1) & (2) we obtain,

Diagram For Case 2

t = AB/v_mwcosθ + ((v_w - v_mwsinθ)/v(v_mvcosθ))

=> t = AB[(1+v_w/v)secθ/v_mv - tanθ/v]

=> t = d/v_mv[(1+v_w/v)secθ/v_mv - tanθ/v]

Putting dt/dθ = 0, For minimum t we get,

dt/dθ = d/dθ[d/v_mv (1+v_w/v) secθ/v_mv - tanθ/v]

= [secθ/v_mv - tanθ/v (1+v_w/v) (sec2θ)/v] = 0

=>tanθ/v_mv (1+v_w/v) secθ/v

=> sin θ = (v_mw/v+v_w)

=> θ = sin^-1(v_mw/v+v_w)

This expression is obviously true when v_mw < v + v_w.

Velocity of Separation/Approach, Relative Angular Velocity

Let thane be two particles A and B with velocity 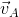$\vec{v}_{A}$ and $\vec{v}_{B}$ at any instant as visualized from ground frame.

If we visualize the motion of B from frame of A the velocity of particle B would be $\vec{v}_{B} - \vec{v}_{A}$ .

Velocity of Separation

If α, β be the angle made with line AB,

then, V_B cos β - V_A cos α is relatively velocity of B w.r.t. A along line AB.

If V_B cos β - V_A cos α > 0; it is called as velocity of separation.
If V_B cos β - V_A cos α < 0; it is called as velocity of approach.

V_B sin β - V_A sin α is relative velocity of B w.r.t. A along direction perpendicular to AB. If length of AB is,

then, angular velocity B w.r.t. A is (V_B sinβ - V_Asinα)/l

and relative angular velocity = (V_B sinβ - V_Asinα)/l.

The analytical method for determination of relative velocity of one body with respect to another which is discussed here is to general nature. This treatment is valid for motion in two dimensions and in three dimensions also.
Relative velocity of a body A with respect to another body B, when both are in motion, is the velocity with which A appears to move to B.
Relative velocity of a body ‘B’ w.r.t. a body ‘A’, when both are in motion, is the velocity with which ‘B’ appears to move to ‘A’.

Question 1

A body dropped from a height h with initial velocity zero, strikes the ground with a velocity 3 m/s. Another body of same mass dropped from the same height h with an initial velocity of 4 m/s. Find the final velocity of second mass, with which it strikes the ground:

(a) 3 m/s (b) 4 m/s

Question 2

From building two balls A and B are thrown such that A is thrown upwards and B downwards (both vertically). If V_A and V_B are their respective velocities on reaching the ground, then:

(a) V_B > V_A (b) V_A = V_B

Question 3

If a car at rest accelerates uniformly to a speed of 144 km/h in 20 sec, it covers a distance of:

(a) 20 cm (b) 400 cm

Question 4

A car, moving with a speed of 50 km/hr, can be stopped by brakes after atleast 6 m. If the same car is moving at a speed of 100 km/hr, the minimum stopping distance is:

(a) 12 m (b) 18 m

Q.1	Q.2	Q.3	Q.4
c	b	b	c

Related Resources

You might like to refer Motion in Two Dimensions.
For getting an idea of the type of questions asked, refer the Previous Year Question Papers.
Click here to refer the most Useful Books of Physics.
To get answer to any question related to Relative Motion click here.

To read more, Buy study materials of Kinematics comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Physics here.