Banking of Roads

 

Table of Content

Purpose of Banking Skidding How to Avoid Skidding? Overturning Related Resources

Perhaps you have noticed that when a road is straight, it is horizontal too. However, when a sharp turn comes, the surface of the road does not remain horizontal. This is called banking of the roads.

Purpose of Banking

Case I: If coefficient of friction, μ = 0:-

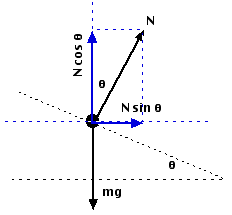
What we really wish is that even if there is no friction between the tyres and the road, yet we should be able to take a round turn. In the given figure Vertical N cos θ component of the normal reaction N will be equal to mg and the horizontal N sin θ component will provide for the necessary centripetal force. [Please note that as we are assuming μ to be zero here, the total reaction of the road will be the normal reaction.] Frictional forces will not act in such a case.

Thus, N cos θ = mg                      .......... (i)

        N sin θ = mv²/r                       .......... (ii)

Dividing equation (ii) by (i), we get

tan θ = v²/rg

where θ is the angle of banking.

Case - II : If coefficient of friction, μ ≠ 0:-

In the above figure shows a section of the banked road and the view of the vehicle form the rear end.

vehicle-form-the-rear-end 

The total forces acting are,

N₁ and N₂ = normal reactions

f₁ and f₂ = frictional forces

mg = weight

r = radius

θ = angle of banking

Let N = Resultant of N₁ and N₂.

f = Resultant of f₁ and f₂.

Let us resolve all the forces horizontally and vertically. As the vehicle has Equilibrium in vertical direction.

so, N cos θ + f sin θ = mg                        ............ (i)

The resultant of horizontal components i.e., (f cos θ + N sin θ), however, this becomes the net external force acting on the vehicle in the radially inward direction of the round-turn. This thus provides for the necessary centripetal force (mv²/r).

Therefore,  f cos θ + N sin θ = mv²/r                     ............ (ii)

Further, if μ is the coefficient of friction, we have

f = μN                                                  ............ (iii)

These are the three basic equations from which, we can find out whatever we want to find out.'

Putting (iii) in (i) gives

N cos θ = μN sin θ + mg

=>N(cos θ - μsin θ) = mg

=> N = mg/cos θ - μsin θ                ...............(iv)

Putting (iii) and (iv) in (ii) gives

μ × mgcos θ/(cos θ - μsin θ) + mgsinθ/(cos θ - μsin θ) = mv²/r

=>    μ mgr cos θ + mgr sin θ = mv² cos θ - μmv² sin θ

Thus, tan θ = (v² - μrg)/(rg + μv²)               ............... (A)

or     v² = rg(μ+ tanθ)/(1-μtanθ)                ................ (B)

(A)    Gives the angle of banking for the maximum velocity v and (B) gives the value of the maximum velocity which the vehicles should be allowed on a road banked at an angle θ.

 Notes : 1. The value of μ is the minimum value of μ required. The value of v is the maximum allowable velocity.

Therefore, the best angle of banking θ so that there is absolutely nil wear and tear due to frictional force for the given values of v and r can be determined by putting μ = 0 in this formula.

If we put μ = 0 in formula (A), we get

tan θ = v²/rg

Further, for zero frictional wear and tear, the velocity for the given values of θ and r will be v = √rgtanθ.

Skidding

Let us consider the situation in the figure. You are cycling fast on road I. You then want to take a turn to go to road II. However, due to big leak of mobile oil from some truck, the portions of the roads within the area ACBD have become slippery. You do not know about it. You are cycling fast. When you reach the line AC, you turn the handle mounted on the front wheel towards road II. What will happen? Will you be able to take the turn? No, you won't be. Although your front wheel is aligned to go towards road II, you still continue to go straight to road III. This is called skidding. You will skid.

The tendency to slip transverse (transverse means across) to the intended line of run, is called skidding. Thus as soon as you turn the handle of your cycle (or the driving wheel in a motor car), skidding will try to occur. If there is enough friction, this start of skidding brings into action a frictional force between the road and the bottom surface of the wheels of the vehicle. This frictional force then provides for the necessary centripetal force required to negotiate the turn. If friction is not enough, skidding will start which will not let you take the turn in a normal way. Skidding will also cause additional friction wear and tear of the tyres of your vehicle.
 

How to Avoid Skidding?

Let us consider the situation given in the figure. Let r is the radius of turn which you have to take. N₁ and N₂ are normal reactions mg the weight and F₁, F₂ the frictional forces on the inside and outside wheels.

So, (N₁ + N₂) = mg                          ......... (i)

Thus, F₁ + F₂ = μ(N₁ + N₂) = μgm         ......... (ii)

This must be greater than or equal to the centripetal force required.

Therefore, μmg > mv²/r

or, v < √μrg

or, V_max = √μrg

If the velocity of the vehicle is more than √μrg, it will skid.

Overturning

You may have seen overturned trucks lying on the road. Such heavily loaded trucks! Who could have overturned them!! Overturning occurs on the roads when the trucks try to change directions, take sharp turns. Overturning occurs, more after, in case of vehicles which have greater height or whose center of gravity are much high up from the surface of roads.

Let us first consider why over turning would take place at all. Suppose a heavily loaded truck is going straight. Suddenly it takes a sharp turn towards its left. Now what actually happens is that while the upper portion of the truck still tends to go straight because of its inertia (Newton's first law of motion), the lower portion starts going towards left because you have turned the driving wheel accordingly.

Thus, if the inertial forces on the upper portion are much height, they provide so much torque on the truck at its center of gravity that overturning takes place.

Thus overturning always takes place by lifting off the inner wheels from the ground on the curved path.

Limiting case when a four wheeler just begins to overturn on a plain horizontal road:-

Let, Mg = weight

N = Total normal reaction = N₁ + N₂

F = Total friction force

v = velocity

r = radius of the round

2a = distance between inner and outer wheels.

G = center of gravity

h = height of center of gravity from Earth. Frictional force F will provide for the necessary centripetal force.

Therefore,  F = mv²/r                               ............... (i)

When the vehicle just begins to overturn, the inner wheels will just begin to lift off from the ground. Their pressure on ground will become zero, so the reaction N₁ on the inner wheels will become zero.

Thus, N₁ = 0

N₁ + N₂ = N₂ = mg

Let us take moments about G

N₂ × a = F × h

Putting (i) and (iii) in (iv) gives

mg × a = mv²/r × h, or v

i.e., v_max = √rga/h

 If speed goes beyond it, the vehicle will overturn.

Minimum μ required to prevent overturning

We know frictional force is μN.

=>     F = μN = μmg                                     ............ (v)

Putting equation (v) in (i) gives

μmg = mv²/r,

Or μ = μ_min = v²/rg

 F = mv²/r = mω²r

Centripetal force is not a new kind of force. It is the radial component of the net force acting on the particle moving along a circle. Centrifugal force is a type of pseudo force used by an observer moving in a circle. Numerically, it is equal to the centripetal force but is oppositely directed if observer and the body both are moving on same circle as a single unit.

The banking angle is the angle at which the vehicle is inclined about its longitudinal axis with respect to the plane of its curved path. If the force of friction is not strong enough, the vehicle will skid. Even if there is very little force of friction the vehicle can still go round the curve with no tendency to skid. Roads are banked because of the inertia of vehicles driving on the road.

Problem 1:-

A curve has a radius of 50 meters and a banking angle of 15º. What is the ideal, or critical, speed (the speed for which no friction is required between the car's tires and the surface) for a car on this curve?

Solution:-

Here, radius of curve, r = 50 m

banking angle, θ = 15º

free-fall acceleration, g = 9.8 m/s²

We have to find out the ideal speed v (the speed for which no friction is required between the car's tires and the surface)

From the free-body diagram for the car:-

F_net = F_centripital

mg tanθ = mv²/r

v² = rg tanθ

v = √rg tanθ

  = √(50 m) (9.8 m/s²) (tan 15º) = 11 m/s

If the car has a speed of about 11 m/s, it can negotiate the curve without any friction.

____________________________________________________________________________________________

Problem 2:-

A 1200 kg automobile rounds a level curve of radius 200 m, on a unbanked road with a velocity of 72 km/hr. What is the minimum co-efficient of friction between the tyres and road in order that the automobile may not skid. (g = 10 m/s²)

Solution:-

In a unbanked road, the centripetal force is provided by the frictional force.

So,  f_friction = mv²/r But f_{limiting friction} > f_friction

 or, μmg = f_friction or μmg = mv²/r

So, μ_min = v²/gr = (20×20)/(10×200) = 0.2.

The bank angle is the angle at which the vehicle is inclined about its longitudinal axis with respect to the plane of its curved path.

If the force of friction is not strong enough, the vehicle will skid.

even if there is very little force of friction the vehicle can still go round the curve with no tendency to skid.

Roads are banked because of the inertia of vehicles driving on the road. 

________________________________________________________________________________________

Problem 3:-

A turn of radius 100 m is being designed for a speed of 25 m/s. At what angle should the turn be banked?

Solution:-

Here, radius of turn, r = 100 m

speed of the car, v = 25 m/s

free-fall acceleration, g = 9.8 m/s²

We have to find out the bank angle, θ.

From the free body diagram of the car,

F_net = F_centripetal

mg tanθ = mv²/r

tanθ = v²/rg

θ = tan^-1(v²/rg)

 = tan^-1 [(25 m/s)²/ (100 m) (9.8 m/s²)] = 33º

So, the banking angle should be about 33º.

Question 1:-

A cyclist is moving with a velocity v turns a circular path of radius r. His inclination with the vertical isd given by

(a) tan θ = v²/rg         (b) tan θ = v²g/r       (c) tan θ = v²rg         (d) none of the above

Question 2:-

A body moving with constant speed in a circular path has

(a) angular momentum              (b) constant acceleration

(c) constant velocity                   (d) no work done

Question 3:-

The work done when a body of mass m revolves with a speed v on a circular path of radius r is

(a) Zero        (b) mvr        (c) mv²         (d) ½ mv²

Question 4:- 

Which of the following statement is not correct in respect of a body in uniform circular motion?

(a) its kinetic energy is constant                (b) its acceleration is constant

(c) its speed is constant                             (d) its angular velocity is constant

Question 5:-

A motor cyclist going round in a circular track at a constant speed has

(a) constant linear velocity                  (b) constant acceleration

(c) acceleration constant magnitude with its direction changing

(d) constant force

Q.1	Q.2	Q.3	Q.4	Q.5
a	d	a	b	c

Related Resources

• You might like to refer Momentum.

• For getting an idea of the type of questions asked, refer the  Previous Year Question Papers.

• Click here to refer the most Useful Books of Physics.

To read more, Buy study material of Laws of Motion comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Physics here.