First Order Reactions

Table of Content

Half-Time or Half-Life Period of a First order Reaction
Some Simple First Order Reactions
Related Resources

A reaction is said to be first order if its rate is determined by the change of one concentration term only.

One can say that a first order reaction is one whose rate varies as 1st power of the concentration of the reactant i.e. the rate increases as number of times as the number of times the concentration of reactant is increased.

Consider the reaction

A → products

Let

[A]_O = Initaial Concentration of A

[A]_t = The concentration of A after time t

For the reaction to be of first order..

$Rate = -\frac{d[A]]}{dt} = k[A]$

$\Rightarrow \frac{d[A]}{[A]} =-kdt$ ...(i)

Intigrating this equation

$\int_{[A]_o}^{[A]} \frac{d[A]}{[A]} =-k\int_{0}^{t}dt$

we get

ln [A] - ln[A]_o = -K(t-0)

$ln\frac{[A]}{[A]_o} = -kt$

$\Rightarrow ln\frac{[A]_o}{[A]} = kt$ …...... (ii)

$\Rightarrow log\frac{[A]_o}{[A]} = \frac{kt}{2.303}$ ...(iii)

$\Rightarrow k= \frac{1}{t}ln\frac{[A]_o}{[A]}$ ....(iv)

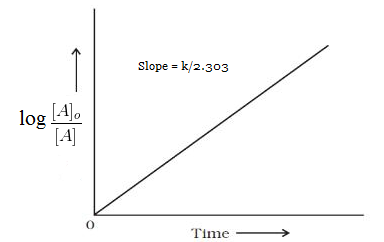
On comparing the equation number (ii) with equation of straight line i.e. y=mx+c we come to know that , If we plot a graph between log [A]_o/[A] vs t, the slope of line= k/2.303

Refer to the following video for first order reactions

Unit of rate constant for first order reaction ( k) = min^–1or s^-1

The rate constant of a first order reaction has only time unit. It has no concentration unit.
This means the numerical value of k for a first order reaction is independent of the unit in which concentration is expressed.
If concentration unit is changed the numerical value of k for a first order reaction will not change.
However, it would change with change in time unit. Say, k is 6.0 $\times$ 10^–3 min then it may also be written as 1 $\times$ 10^–4 s^–1 i.e. numerical value of k will decrease 60 times if time unit is changed from however to minute or from minute to second.

Half-Time or Half-Life Period of a First order Reaction

The half-time of a reaction is defined as the time required to reduce the concentration of the reactant to half of its initial value. It is denoted by the symbol t_1/2. Thus,

For first order reaction, we know that

$k= \frac{1}{t}ln\frac{[A]_o}{[A]}$

at half life of reaction,

t = t_½& [A] = [A]_o/2

$k= \frac{1}{t_1_/_2}ln\frac{[A]_o}{\frac{[A]_o}{2}}$

$\Rightarrow t_{1/2} = \frac{0.693}{k}$

Since k is a constant for a given reaction at a given temperature and the expression lacks any concentration term so half-time of a 1st order reaction is a constant independent of initial concentration of reactant.
This means if we start with 4 mole L^–1 of a reactant reacting by first-order kinetics and after 20 minute it is reduced to 2 mole L^–1 will also be 20 minute.
That is, after 20 minutes from the start of reaction the concentration of the reactant will be 2 mole L^–1, after 40 minutes from the start of reaction of concentration is 1 mole L^-1. After 60 minutes from the start of reaction the concentration of the reactant will be reduced to 0.5 mole L^–1. In other words, if during 20 minute 50% of the reaction completes, then in 40 minute 75%, in 60 minute 85.5% of the reaction and on will complete as shown with following plot.

Examples of first order reactions

Decomposition of H₂O₂ in aqueous solution

H₂O₂ → H₂O + 1/2 O₂

Hydrolysis of methyl acetate in presence of mineral acids.

CH₃COOCH₃ + H₂O → CH₃COOH + CH₃OH

Inversion of cane sugar in presence of mineral acids.

C₁₂H₂₂O₁₁ + H₂O $\overset{H^+}{\rightarrow}$ C₆H₁₂O₆ + C₆H₁₂O₆

Decomposition of ammonium nitrite in aqueous solution.

NH₄NO₂ → N₂ + 2H₂O

Hydrolysis of diazo derivatives.

C₅H₅N = NCl + H₂O → C₆H₅OH + N₂ + HCl

Note: In case of gases, pressure can be used in place of concentration.

Some Simple First Order Reactions

As we have to generally deal with only first order reactions, we examine some of these reactions from the point of calculating the rate constant based on different experimental data.

Now we present several problems in which we shall learn how to calculate the rate constant of reactions based on the variety of data given.

We are given a first order reaction A → B+C where we assume that A,B and C are gases. The data given to us is

Time	0	t
Partial pressure of A	P₁	P₂

And we have to find the rate constant of the reaction.

Since A is a gas and assuming it to be ideal, we can state that P_A = [A]RT

[From PV = nRT]. \ at t = 0, P₁ = [A]_o RT and at t = t, P₂ = [A]_tRT. Thus the ratio of the concentration of A at two different time intervals is equal to the ratio of its partial pressure at those same time intervals.

Now we consider the same reaction with different set of data A → B +C

Time	0	t
Total pressure of A +B+C	P₁	P₂

Find k.

In this we are given total pressure of the system at these time intervals. The total pressure obviously includes the pressure of A, B and C. At t = 0, the system would only have A. Therefore the total pressure at t = 0 would be the initial pressure of A \ P₁ is the initial pressure of A. At time t let us assume that some moles of A decomposed to give B and C because of which its pressure is reduced by an amount x while that of B and C is increased by x each. That is

Now let us move on to the next case. In this case we have A → B +C

Time	t	$\infty$
Total pressure of A+B+C	P₂	P₃

Find k.

Here $\infty$ means that the reaction is complete. Now we have

Now let us assume that A,B and C are substances present in a solution.

From a solution of A, a certain amount of the solution (small amount) is taken and titrated with a suitable reagent that reacts with A. The volume of the reagent used is V₁ at t = 0 and V₂ at t = t

Time	0	T
Volume of reagent	V₁	V₂

The reagent reacts only with A. Find k.

It can be understood that the volume of the reagent consumed is directly proportional to the concentration of A. Therefore the ratio of volume of the reagent consumed against A at t=0 and t = t is equal to [A]₀ /[A]

Now consider this situation A → B+C

Time	T	$\infty$
Volume of reagent	V₂	V₃

Reagent reacts with all A,B and C and have ‘n’ factors in the ratio of 1:2:3 with the reagent. Find k.

Now, we will consider a reaction A $\overset{D}{\rightarrow}$ B+C which is catalysed by D. We will assume in this problem that the concentration of the catalyst remains constant throughout. The data given to us is

Time	0	t	$\infty$
Volume of reagent	V₁	V₂	V₃

The reagent reacts with all (A,B,C and D). Assume that ‘n’ factor of A,B and C are in the ratio of 1:1:1 and that of D is not known. Find k.

Let V_A be the volume of the reagent required by A initially and V_D be the volume required
by D.

\V₁ = V_A + V_D

V₂ = (V_A – x) + x + x +V_D (x is the volume of the reagent required for those moles of A that have reacted to give B and C).

V₃ = 2V_A+V_D

We can see that, V₃–V₁ = V_A

Now we shall see how to find the rate constant of a reaction using a very different set of data.

There are some organic compounds which have a property of rotating a plane polarized light in a particular direction by a particular value. The compounds are called optically active compounds. One reaction in which an optically active substance converts to some other optically active substance is,

Sucrose $\overset{H^+}{\rightarrow}$ Glucose + Fructose

Sucrose, Glucose and Fructose are all optically active and while the first two compounds are dextro rotatory (rotating the plane polarised light in the right hand direction and the last is laevo rotatory (rotating the plane polarized light in the left hand direction). All the three compounds rotate the plane polarised light by different angles and their rotation is directly proportional to concentration.

Now the problem is S → G + F and the data is

Time	0	t
Rotation of sucrose	r₀	r_t

Find k.

Let the rotation of Sucrose be r₁° per mole and the initial moles of Sucrose be a.

r₀ = ar₁⁰

Let the moles of Sucrose that is converted to Glucose and Fructose be x.

Question 1:

Rate of first order reaction.

a. depends on concentration of reactants.

b. depends on concentration of products.

c. depends on concentration of both reactant and product.

d. does not depend on concentrations.

Question 2:

Unit of rate constant for first order reaction is

b. mol² L^-1 time^-1.

c. mol L^-1 time^-1.

d. time^-1.

Question 3:

If we plot ln [A]_o/[A] vs t, we get a straight line with slope =

a. rate constant

b. arrhenius constant

c. temperature coefficient

d. equilibrium constant

Question 4:

For zero order reaction d[A] =

a. -kdt

b. -k[A]₀

c.-k[A]₀dt

d. -k[A]⁰

Q.1	Q.2	Q.3	Q.4
a	d	a	a

Related Resources

Click here to get detailed Syllabus of IIT JEE
Refer to the Books of Chemistry for IIT JEE
Click here to refer Zero Order Reaction

To read more, Buy study materials of Chemical Kinetics comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Chemistry here.

Live courses Ask question

First Order Reactions

Table of Content

Half-Time or Half-Life Period of a First order Reaction

Examples of first order reactions

Some Simple First Order Reactions

T

Related Resources