Ellipse

 

Table of Content

History of an Ellipse Meaning of an Ellipse Ellipse in Conic Sections Is an Ellipse a circle? Terms related to Ellipse What is the focus of an Ellipse? Properties of an Ellipse Focus of an Ellipse Eccentricity of an Ellipse Directrix of an Ellipse Latus rectum of an Ellipse Principal Axis Focal Parameter Area of an Ellipse Circumference of an Ellipse Equation of an Ellipse General form of equation of an Ellipse Standard form of equation of an Ellipse How do you find the foci of an Ellipse? Graph of Ellipse

 

History of an Ellipse

It was Menaechmus who first studied about ellipse. Then Euclid investigated and wrote about it .Its name was provided by Apollonius. Pappus considered the focus of an ellipse  and the directrix of an ellipse. It was in 1602 when Kepler thought that the orbit of Mars was oval and studied about it so that he discovered that the ellipse with the Sun was at one focus. The word "focus" was also introduced by Kepler and he published it in 1609. In 1705, Halley displayed that the comet which was named after him was also moved in an elliptical orbit around the Sun .an ellipse rotated around its minor axis and gives an oblate spheroid, and an ellipse revolved around its major axis and gives a prolate spheroid.

Meaning of an Ellipse

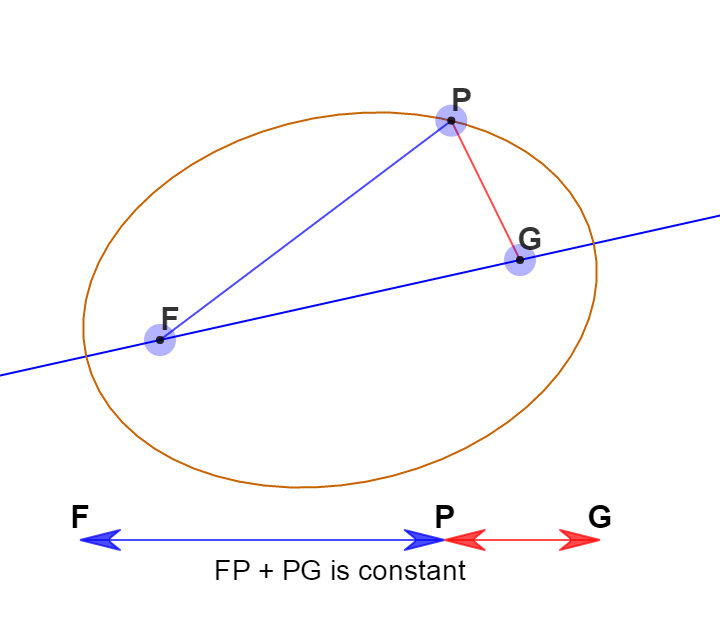
an Ellipse is an oval shaped closed curve. In an Ellipse the sum of the distance from the two fixed points (focus) together called Foci to any point on the ellipse is constant.

 

Ellipse in Conic Sections

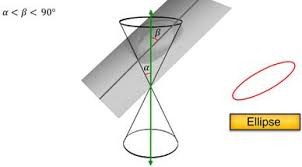
Ellipse is formed in conic sections when a plane intersects the right circular cone in such a way that the angle between the axis and the plane is greater than the vertex angle, that is, α < β < 90°.
 

Is an Ellipse a circle?

Circle is a special form of an ellipse which has both the focal points at the same point. As in the ellipse the distance of the summation of two focal points to any point on ellipse is persistent and equal to major axis, in circle it is equal to diameter as it has both the focal points at the same point i.e. the center of the circle. It’s both the major and the minor axis are of same length. In circle the plane is parallel to the base of the cone but in ellipse it is not parallel to the base of the cone.
 

Terms related to Ellipse

• Center- It is the point where major and minor axis intersects each other. The midpoint of the connecting two foci line segment is the center.

• Focus - There are two focal points on the major axis which defines the ellipse. These are at the same distance to the both sides from the center.

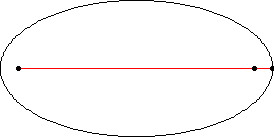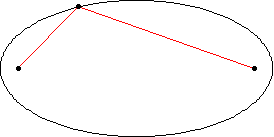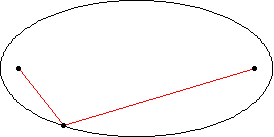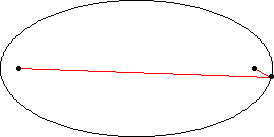
• Major Axis - It is the lengthiest diameter of the ellipse. It has the end points on the widest part of the ellipse and passes through the center.

• Minor Axis – It is the shortest diameter of the ellipse. It is the perpendicular bisector of the major axis. It has the end points on the narrow part of the ellipse and passes through the center.

• Semi Major Axis - It is the half part of the major axis. It is also called the Major Radius of the Ellipse.

• Semi Minor Axis - It is the half part of the minor axis. It is called the Minor Radius of the Ellipse.

• Vertices - The four points where the major and minor axis touches the ellipse are the vertices. The end points of major axis are generally called Vertex and the end points of minor axis are generally called Co-vertex.

• Chord - It is a line segment that has both the end points on the ellipse. Major axis is also the chord which is the longest one in an ellipse.

• Arc -  an arc is the two points on the ellipse which connect the circumference of the circle.

• Tangent - It is a line which touches the ellipse at one point only.
   

What is the focus of an Ellipse?

The two focus points together called Foci are those special points which define an ellipse.

• The ellipse is defined as the set or locus of all points on a plane the sum of whose distances from two fixed points called Focus is constant.

• The foci are always on the major axis.

• Both the focus is at the same distance from the center.

• The line segment or the distance from the center to any of the focus is also called Linear Eccentricity.
   

Properties of an Ellipse

Focus of an Ellipse

Focus is a point from which the distance is measured to form conic. The ellipse has two focus points together called Foci. The midpoint of the two foci is the center of the ellipse. It is the special point which helps in defining ellipse. The summation of the distance from any fixed point on a plane to the two foci is always constant."
 

Eccentricity of an Ellipse

Eccentricity is the factor related to conic sections which shows how circular the conic section is. More eccentricity means less spherical and less eccentricity means more spherical. It is denoted by“e”.

The eccentricity of an ellipse is showed by the ratio of the distance between the two foci, to the size of the major axis,

 e = 2f/2a = f/a.

where e = Eccentricity, f =  The distance from the center to any one of the foci and a = The semi major axis.

The eccentricity of an ellipse is between 0 and 1 (0 < e < 1). If the eccentricity is zero the foci match with the center point and become a circle. If the eccentricity moves toward 1, the ellipse gets a more stretched shape.
 

Directrix of an Ellipse

Directrix is the line which is parallel to the minor axis of the ellipse and related to both the foci of the ellipse. The distance from any point A on the plane to the focus F is a constant fraction of that point's perpendicular distance to the directrix, that is, e = AF/AD. This ratio is also the eccentricity of the ellipse.
 

Latus rectum of an Ellipse

It is the line parallel to directrix and passes through any of the focus of an ellipse. It is denoted by “2l”.

In an ellipse, latus rectum is 2b²/a (where a is one half of the major diameter and b is the half of the minor diameter).

The half of latus rectum till its intersection point with the major axis is the semi latus rectum. It is denoted by “l”.
 

Principal Axis

The line which joins the two foci of the ellipse is the principal axis and the midpoint of that line segment is the center.
 

Focal Parameter

The distance between the directrix and the focus is the focal parameter. It is denoted by “p”.
 

Area of an Ellipse

Area of an ellipse is:

            A = πab

where A = Area of an ellipse, a = Length of semi major axis and b = Length of semi minor axis.

This is same as area of circle, as area of circle is r² = π × r × r, where r is the radius of the circle.

and in ellipse a is the major radius and b is the minor radius. So the area of an ellipse is π × a × b.
 

Circumference of an Ellipse

Unlike, circle, it is not so easy to calculate the perimeter of an ellipse.

The approximate value of the circumference of ellipse could be calculated as:

Where, a is the major radius and b is the minor radius.

Equation of an Ellipse

General form of equation of Conics

Ax² + Bxy + Cy² + Dx + Ey + F = 0

The expression B² - 4AC is the discriminant which is used to determine the type of conic section represented by equation.

If equation fulfills these conditions, then it is an ellipse.

B² - 4AC< 0,either B ≠ 0 or A ≠ C

Example

Given equation is x² + 2y² + 4x + 2y – 27 = 0, find whether it is the equation of ellipse or not?

Solution:

Here A = 1, B = 0, C = 2

Determinant will be B² - 4AC

= 0² - 4(1) (2) = – 8

This shows that B² - 4AC < 0, and A ≠ C so this is an ellipse or in other way we can say that Both variables are squared with the same sign, but they aren't multiplied by the same number, so this is an ellipse.
 

Standard form of equation of an Ellipse

Cartesian coordinates are the points on a plane with a pair of numerical coordinates which represented by (x, y).

• If the center is (0,0): If the center of an ellipse lies on the origin of the plane, then the coordinates of the center of the ellipse (h, k) will be (0, 0). (x, y) are the coordinates of any point on the ellipse. So the equation will be:

Horizontal Ellipse

where a >b, a is the semi-major axis and b is the semi-minor axis, this shows that the major axis lies on the x-axis.

Vertical Ellipse

​

where a > b, this shows that the major axis lies on the y axis.

• If the center is (h,k): If the center is not on the origin of the plane, then the equation will be-

Horizontal Ellipse

where a >b, a is the semi-major axis and b is the semi-minor axis, (h, k) are the coordinates of the center point of the ellipse. The major axis lies on the x axis.

Vertical Ellipse

where a > b, this shows that the major axis lies on the y axis.
 

How do you find the foci of an Ellipse?

Let a is the length of the semi major axis, b is the length of semi minor axis and c is the length of the distance between center and any of the foci.

According to the formula of Pythagoras theorem we got the formula

So we can easily calculate the foci of the ellipse using the above formula.

Example

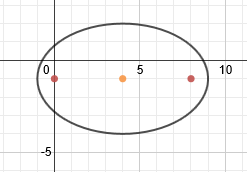
Find the foci of the given equation?

Solution:

 As it is given that  a² = 25 tha is, a = 5

b² = 9 that is, b = 3

The center of the ellipse is at the points (4,-1)

To find the foci we will put the values in the formula of foci.

c² = a² - b²

= 25 – 9

= 16

c = 4

We can easily find the coordinates of the foci by adding 4 to the center point.as a>b so the major axis is on the x-axis, i.e. it is a horizontal ellipse. So we will add 4 to the x coordinate in the center coordinates to the left and right, which is (4,-1).

The coordinates of the foci will be (0,-1) and (8,-1) 
 

Graph of Ellipse

To draw a graph of ellipse we must know the center of the ellipse and the foci. We will use the standard form of equation to draw the graph as it is also known as radius centered equation as it tells us about the coordinates of the center of the ellipse and the foci of the ellipse..

• If the center is (0,0): It is easy to draw an ellipse if its center is at the origin.

Example

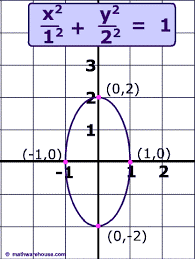Draw the graph of the ellipse with equation 

Solution:

Here we know that the (h, k) = (0, 0), so the center is at the origin. The a should be greater than b and a is the coordinate below y so this shows that the major axis will be on y axis, that is, it is a vertical ellipse.

a =2 and b =1

Now we will count till 2 on y axis up and down and count till 1 on x axis both left and right, then we will make the curve joining all the four points and we will get the ellipse for the equation.

 

• If the  center is away from the origin: If we have to draw a ellipse which has its center away from the origin i.e. the center point must be something (h,k).Then we will plot the center at (h,k) then count till a on the major axis and till b on the minor axis and will draw an ellipse accordingly.

Example

Draw a graph of an ellipse with equation

Solution:

Here we know the center of the ellipse by the equation, (h, k) = (2, -1), a = 4 and b = 3. This equation shows that it is a horizontal ellipse as major axis on the x axis.

So first we will first plot the center of the ellipse on the graph with the coordinates (2, - 1). Then we will count till 4 on the x axis on both the left and right side.

Now we will count till 3 on the y axis both up and down.

After plotting all the points we will make a curve joining all the points which will turn out to be a horizontal ellipse.

Example

Find the foci of the given equation and then draw the graph.

Solution:

 With the formula we will find the foci of the given equation.

Here, (h, k) = (4,-1), a = 5, b = 3

c² = a² - b²

= 25 – 9 = 16

c = 4

We can easily find the coordinates of the foci by adding 4 to the center point.as a>b so the major axis is on the x-axis, that is, it is a horizontal ellipse. So we will add 4 to the x coordinate in the center coordinates to the left and right, which is (4,-1).

The coordinates of the foci will be (0,-1) and (8,-1)

The graph of the above equation and the points of foci are in the graph below:

 

More Readings

Ellipse

To read more, Buy study materials of Ellipsecomprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.