• Algebra
• OFFERED PRICE: Rs. 2,332
• View Details

Circular Permutations

 

The arrangements we have considered so far are linear. There are also arrangements in closed loops, called circular arrangements.

Consider four persons A, B, C and D, who are to be arranged along a circle. It's one circular arrangement is as shown in adjoining figure.



Shifting A, B, C, D one position in anticlockwise direction we will get arrangements as follows.



Arrangements as shown in figure (I) (II) (III) and (IV) are not different as relative position of none of the four persons A, B, C, D is changed. But in case of linear arrangements the four arrangements are.



Thus, it is clear that corresponding to a single circular arrangement of four different things there will be 4 different linear arrangements. Let the number of different things be n and the number of their circular permutations be x.

Now for one circular permutation, number of linear arrangements is n

For x circular arrangements number of linear arrangements

                                                = nx.                 .............. (1)

But number of linear arrangements of n different things

                                                = n!                  .............. (2)

From (1) and (2) we get

                                           Nx = n! => x = n!/n = (n - 1)!.

Suppose n persons (a1, a2, a3, ......, an) are to be seated around a circular table. There are n! ways in which they can be seated in a row. On the other hand, all the linear arrangements

        a1, a2, a3, ........., an

        an, a1, a2, ........., an-1

        an-1, an, a1, a2, ........., an-2

        ................................................

        ................................................

        a2, a3, a4, ........., a1

will lead to the same arrangements for a circular table. Hence one circular arrangement corresponds to n unique row (linear) arrangements. Hence the total number of circular arrangements of n persons is  = (n - 1)!.

In other words the permutation in a row has a beginning and an end, but there is nothing like beginning or end in circular permutation. Hus, in circular permutation, we consider one object is fixed and the remaining objects are arranged in (n - 1)! ways (as in the case of arrangement in a row).

 

Distinction Between Clockwise and Anti-Clockwise Arrangements

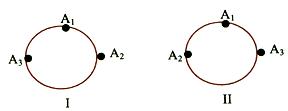
Consider the following circular arrangements:

 

In figure I the order is clockwise whereas in figure II, the other is anti-clock wise. These are two different arrangements. When distinction is made between the clockwise and the anti-clockwise arrangements of n different objects around a circle, then the number of arrangements = (n - 1)!.

But if no distinction is made between the clockwise and anti-clockwise arrangements of n different objects around a circle, then the number of arrangements is  (n - 1)!.

As an example consider the arrangements of beads (all different) on a necklace as shown in figure A and B.



Look at (A) having 3 beads x1, x2, x3 as shown. Flip (A) over on its right. We get (B) at once. However, (A) and (B) are really the outcomes of one arrangement but are counted as 2 different arrangements in our calculation. To nullify this redundancy, the actual number of different arrangements is

(n - 1)!/2.

Note:   (i)   When the positions are numbered, circular arrangements is treated

                    as a linear arrangement.        

               (ii)    In linear arrangements it does not make difference whether

                    the positions are numbered or not.

  

Illustration:

20 persons we invited to a party. In how many ways can they be seated in a round table such that two particular persons sit on either side of the host?

Solution:

After fixing the places of three persons (1 host + 2 persons) and treating them as 1 unit we can arrange the total (20 - 2 + 1) = 19 units in 18! ways. Again these particular persons can sit on either side of the host in 2 ways.

Hence the total number of ways is 18! × 2.

Illustration:

In how many ways 10 boys and 5 girls can sit around a circular table, so that no two girls sit together.

Solution:



10 boys can be seated in a circle in 9! ways. There are 10 spaces between the boys, which can be occupied by 5 girls in 10p5 ways. Hence total number of ways = 9! 10p5 = (9!10!)/5! .

Number of circular permutations of n different things taken r at a time

 =  (if clockwise and anticlockwise orders are taken as different)

 =  (if clockwise and anticlockwise orders are not taken to be different)

Illustration:

In how many ways can 20 persons be seated round a table if there are 9 chairs?

Solution:

In case of circular table the clockwise and anticlockwise arrangements are different.

Hence the total number of ways = 

Illustration:

How many necklaces of 10 beads each can be made from 20 beads of different colours?

Solution:

In case of necklace there is no distinction between the clockwise and anticlockwise arrangements.  Then the required number of circular permutations

  = 19!/(10!)2 .

IIT JEE and AIEEE study material is available online free of cost at askIITians.com. Study Physics, Chemistry and Mathematics at askIITians website and be a winner. We offer numerous live online classroom courses as well for live online IIT JEE preparation - you do not need to travel anywhere any longer - just sit at your home and study for IIT JEE live online with askIITians.com.

To read more, Buy study materials of Permutations and Combinations comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.

• Complete JEE Main/Advanced Course and Test Series
• OFFERED PRICE: Rs. 15,900


• View Details Xpress Buy

Course Features

• 731 Video Lectures
• Revision Notes
• Previous Year Papers
• Mind Map
• Study Planner
• NCERT Solutions
• Discussion Forum
• Test paper with Video Solution